Cuando se analizan las principales características de las fibras ópticas, rápidamente se establece la diferencia entre fibras multimodo y fibras monomodo. De la misma manera, cuando se consultan las características de las fibras multimodo, fácilmente se observa que las más utilizadas son las de 62,5/125 y las de 50/125, siendo estos números los diámetros en micras (milésimas de milímetro) del núcleo y del revestimiento respectivamente.
Fibras ópticas multimodo de Optral (www.optral.es)
Sin embargo, al analizar las características de las fibras monomodo se observa que, al contrario que en las fibras multimodo, en ningún momento se indica el diámetro del núcleo de la fibra.
Propiedades geométricas/mecánicas de las fibras monomodo G.652 (www.optral.es)
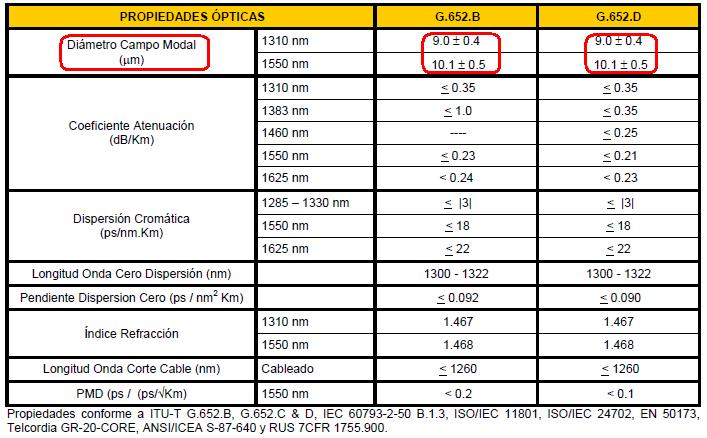
En el cuadro de propiedades geométricas y mecánicas de las fibras monomodo se indican con precisión los diámetros del revestimiento y del recubrimiento primario, pero no aparece el dato correspondiente al núcleo. ¿Es un error? No parece, ya que en otros catálogos de otros proveedores de fibras ópticas sucede lo mismo. Sin embargo, al analizar los datos correspondientes a las propiedades ópticas, aparece un dato denominado Diámetro Campo Modal cuyas dimensiones en micrómetros coinciden razonablemente con el diámetro esperado para una fibra óptica monomodo.
Propiedades ópticas de las fibras monomodo G.652 (www.optral.es)
No obstante, hay algo que llama poderosamente la atención y es que, al parecer, este supuesto diámetro del núcleo cambia con la longitud de onda utilizada, lo cual da la impresión de ser algo imposible. Y efectivamente es así. El diámetro físico del núcleo es siempre el mismo, ya que es inherente al proceso de fabricación de las propias fibras monomodo, pero cuando la luz circula por el interior de estas fibras monomodo no lo hace solamente por el núcleo, sino que una parte significativa lo hace por el revestimiento o cladding. Por lo tanto, a efectos de acoples entre fibras no importa tanto el diámetro físico del núcleo como el diámetro efectivo ocupado por la luz al propagarse por la fibra óptica. Esto es lo que se conoce como diámetro de campo modal, el cual incluye al núcleo y a una pequeña parte del revestimiento.
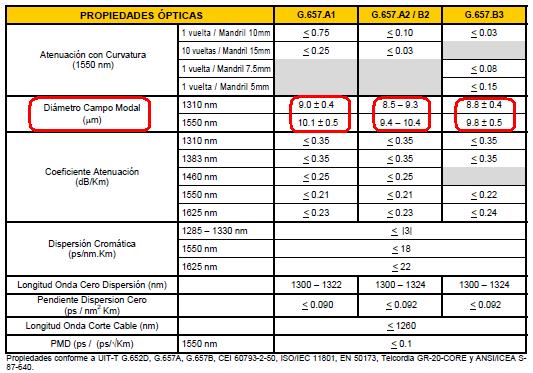
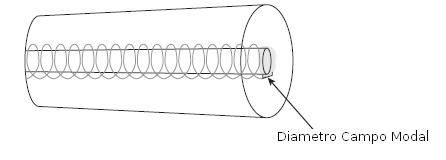 En la imagen anterior se muestra la forma en que se propaga la luz por el interior de las fibras monomodo. En estas fibras solo existe un único modo (equivalente, de alguna manera, a un único rayo de luz) que avanza tanto por el núcleo como por el revestimiento, y la cantidad de luz que se propaga por el revestimiento o cladding depende de la longitud de onda utilizada, lo cual hace que el diámetro de campo modal dependa a su vez de dicha longitud de onda utilizada. En la siguiente tabla se muestran las propiedades ópticas de otro tipo de fibras monomodo, la G.657 de Optral. Se aprecia de nuevo que el diámetro de campo modal cambia significativamente con la longitud de onda utilizada.
En la imagen anterior se muestra la forma en que se propaga la luz por el interior de las fibras monomodo. En estas fibras solo existe un único modo (equivalente, de alguna manera, a un único rayo de luz) que avanza tanto por el núcleo como por el revestimiento, y la cantidad de luz que se propaga por el revestimiento o cladding depende de la longitud de onda utilizada, lo cual hace que el diámetro de campo modal dependa a su vez de dicha longitud de onda utilizada. En la siguiente tabla se muestran las propiedades ópticas de otro tipo de fibras monomodo, la G.657 de Optral. Se aprecia de nuevo que el diámetro de campo modal cambia significativamente con la longitud de onda utilizada.
Propiedades ópticas de las fibras monomodo G.657 (www.optral.es)
Cuando se intenta justificar por qué la luz se propaga de tal manera en las fibras monomodo, se debe de tener en cuenta que no es posible determinar la forma de propagación de la luz en las fibras ópticas monomodo mediante los procedimientos basados en la óptica geométrica, tal y como se puede hacer en las fibras multimodo. Cuando se analiza la propagación de la luz en una fibra monomodo es preciso acudir a la teoría ondulatoria, aplicando para ello las Ecuaciones de Maxwell. Ahora bien, realizar el estudio de propagación mediante dichas ecuaciones implica una complejidad matemática notable, fuera del alcance de los contenidos que se imparten a alumnos de ciclos formativos de grado superior y grado medio, y fuera también de los objetivos que se persiguen con los artículos publicados en este blog. Únicamente a modo de ejemplo se muestran a continuación las cuatro ecuaciones de Maxwell:
 Estas ecuaciones permitieron por primera vez unificar los campos eléctricos y los campos magnéticos, estudiados hasta entonces como hechos separados. Además, le permitieron a Maxwell demostrar que siempre que existe un campo eléctrico variable también existe un campo magnético variable y viceversa, constituyendo estos dos campos un campo electromagnético. Una vez establecida la existencia de los campos electromagnéticos, Maxwell demostró matemáticamente la existencia de ondas electromagnéticas, las cuales debían de consistir en ondulaciones de ese campo electromagnético. Finalmente Maxwell propuso que la luz es también una onda electromagnética, es decir, una alteración u ondulación del campo electromagnético que se desplaza a través de dicho campo. Utilizando las ecuaciones de Maxwell se puede calcular de forma rigurosa como se produce la propagación de la luz por cualquier medio, incluidas las fibras ópticas. En cualquier caso, se debe de tener presente que las cuatro ecuaciones de Maxwell, a pesar de su aparente simplicidad, constituyen uno de los logros matemáticos más importantes en la historia de la física, constituyendo además uno de los pilares sobre los que Albert Einstein construyó su Teoría de la Relatividad Especial.
Estas ecuaciones permitieron por primera vez unificar los campos eléctricos y los campos magnéticos, estudiados hasta entonces como hechos separados. Además, le permitieron a Maxwell demostrar que siempre que existe un campo eléctrico variable también existe un campo magnético variable y viceversa, constituyendo estos dos campos un campo electromagnético. Una vez establecida la existencia de los campos electromagnéticos, Maxwell demostró matemáticamente la existencia de ondas electromagnéticas, las cuales debían de consistir en ondulaciones de ese campo electromagnético. Finalmente Maxwell propuso que la luz es también una onda electromagnética, es decir, una alteración u ondulación del campo electromagnético que se desplaza a través de dicho campo. Utilizando las ecuaciones de Maxwell se puede calcular de forma rigurosa como se produce la propagación de la luz por cualquier medio, incluidas las fibras ópticas. En cualquier caso, se debe de tener presente que las cuatro ecuaciones de Maxwell, a pesar de su aparente simplicidad, constituyen uno de los logros matemáticos más importantes en la historia de la física, constituyendo además uno de los pilares sobre los que Albert Einstein construyó su Teoría de la Relatividad Especial.
 La resolución de las ecuaciones de Maxwell para la propagación de la luz en las fibras monomodo, al tratarse de ecuaciones diferenciales, dan lugar a una solución general y a un conjunto de soluciones particulares, las cuales se denominan modos. Cuando se estudia la propagación de la luz por una fibra óptica desde el punto de vista de la óptica geométrica basta con que los rayos introducidos en la fibra lo hagan con un ángulo menor que el ángulo de aceptación máximo. Todos los rayos que entran en la fibra con esa condición se propagarán por el interior de la fibra mediante el fenómeno denominado reflexión total. En cambio, cuando se estudia la propagación de la luz en la misma fibra mediante la teoría de propagación electromagnética, se demuestra que no todos los rayos que entran en la fibra con el ángulo adecuado se propagan a través de ella. Los rayos que si se propagan por el interior de la fibra son los modos y se corresponden con las soluciones particulares a las ecuaciones de Maxwell indicadas anteriormente.
La resolución de las ecuaciones de Maxwell para la propagación de la luz en las fibras monomodo, al tratarse de ecuaciones diferenciales, dan lugar a una solución general y a un conjunto de soluciones particulares, las cuales se denominan modos. Cuando se estudia la propagación de la luz por una fibra óptica desde el punto de vista de la óptica geométrica basta con que los rayos introducidos en la fibra lo hagan con un ángulo menor que el ángulo de aceptación máximo. Todos los rayos que entran en la fibra con esa condición se propagarán por el interior de la fibra mediante el fenómeno denominado reflexión total. En cambio, cuando se estudia la propagación de la luz en la misma fibra mediante la teoría de propagación electromagnética, se demuestra que no todos los rayos que entran en la fibra con el ángulo adecuado se propagan a través de ella. Los rayos que si se propagan por el interior de la fibra son los modos y se corresponden con las soluciones particulares a las ecuaciones de Maxwell indicadas anteriormente.
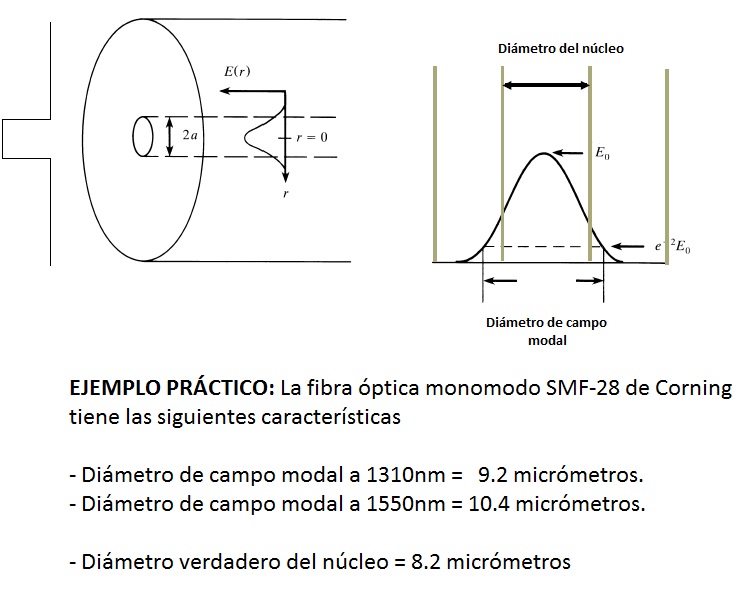
En el caso de las fibras monomodo solo existe un único modo de propagación posible, el modo fundamental, y como ya se ha indicado, avanza por el núcleo de la fibra pero también lo hace en menor medida por el revestimiento. En estos casos, la energía transmitida toma un valor máximo en el centro de la fibra y va disminuyendo de forma gradual hacia el exterior, siguiendo una curva aproximadamente de perfil gaussiano. El lugar donde la potencia transmitida toma un valor de e–² (aproximadamente 0,13) del valor máximo, determina el diámetro de campo modal.
A efectos prácticos, el diámetro de campo modal juega un papel fundamental en los siguientes aspectos:
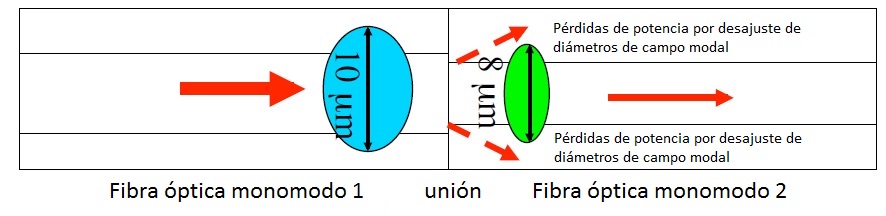
1.- Unión de fibras ópticas monomodo: Es imprescindible que las fibras ópticas monomodo a fusionar o conectar tengan el mismo diámetro de campo modal, a fin de reducir las pérdidas en la unión al mínimo posible.
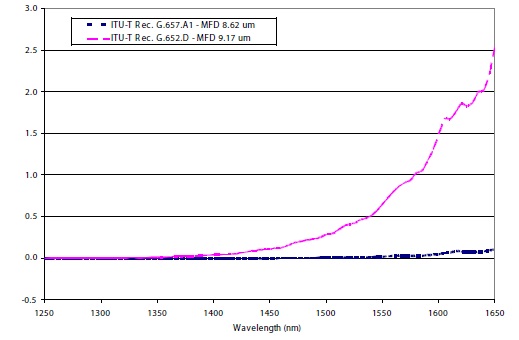
2.- Pérdidas por macrocurvaturas: Las fibras ópticas monomodo son muy sensibles a las pérdidas por macrocurvaturas y estas pérdidas son mayores cuanto mayor es el diámetro de campo modal. En la siguiente imagen se observa como aumentan las pérdidas por macrocurvaturas para dos fibras monomodo con diámetro de campo modal diferente, enrolladas ambas en un cilindro de 20 mm de diámetro. Se aprecia que hasta una longitud de onda determinada las pérdidas por macrocurvaturas son inapreciables en ambas fibras, pero una vez superado esa longitud de onda, las pérdidas aumentan mucho más fuertemente en la fibra monomodo cuyo diámetro de campo modal es mayor, la G.652D (curva de color violeta). En cambio, para la fibra G.657.A1, cuyo diámetro de campo modal es más pequeño y más parecido al diámetro físico del núcleo, las pérdidas por macrobending apenas aumentan, ya que la mayoría de la luz se transmite por el núcleo.
www.corning.com
Estas fibras ópticas monomodo con diámetro de campo modal reducido y por tanto con una transmisión de luz por el núcleo casi total, se denominan fibras ópticas insensibles a curvaturas. Todos los proveedores de fibras ópticas cuentan con uno o varios modelos de este tipo de fibras. Volviendo de nuevo al proveedor Optral, podemos comprobar que dispone de fibras ópticas monomodo compatibles con el estandar G.657, las cuales tienen las siguientes características:
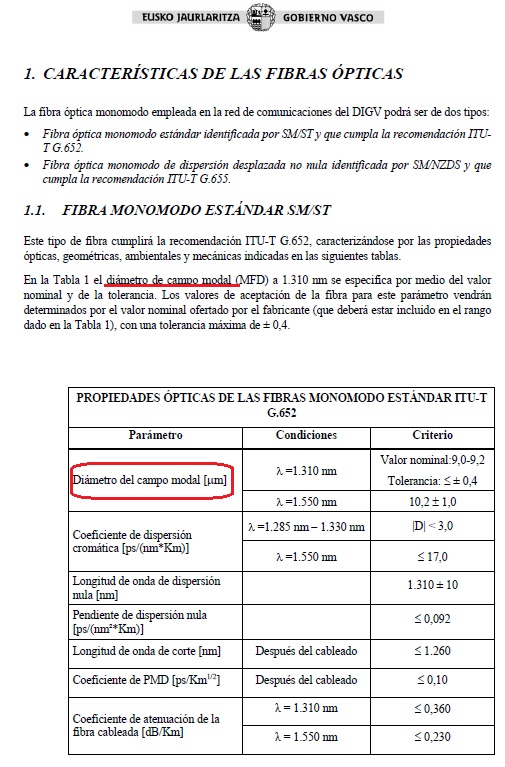
Finalmente, visto todo lo anterior acerca de la importancia del diámetro de campo modal, es importante señalar que en cualquier proyecto de instalación de fibras ópticas monomodo es necesario especificar con claridad el tipo de fibras a utilizar y su diámetro de campo modal. A modo de ejemplo se muestran las especificaciones técnicas requeridas por el Gobierno Vasco para la instalación de la red de fibra óptica correspondiente a las comunicaciones del departamento de interior.




Creo muy buenas las aclaración es realizadas por Enrique, pertenecemos a departamentos de homolgaciones de productos y deja muy claro los errores comunes que se cometen en estos aspectos.
De acuerdo con lo reflejado con Enrique del Rio
Tengo claro que la fibra G.652.D es compatible para fusión con G.657.A2
Pero no encuentro referencia con la compatibilidad de la fibra óptica G.657.A1 y G. 657.A2 para empalme mecánico y por fusión??
La misma duda tengo con la Fibra G. 657.A1 y G.652.D, ¿son compatibles???
Saludos
Los datos que aparecen en la entrada están obtenidos de las web del distribuidor Optral, empresa que diseña, produce y comercializa cables de fibra óptica y también del fabricante Corning, del cual no creo que sea necesario indicar su directa relación con las fibras ópticas. Además, para esta entrada del blog se han consultado los documentos oficiales del ITU-T, en los que se establecen las características mínimas que deben cumplir esos tipos de fibras ópticas. En concreto se ha examinado la recomendación ITU-T G.652 para las fibras G.652D y la recomendación ITU-T G.657 para las fibras G.657 A2 (ambos documentos se pueden obtener fácilmente en Internet).
En dichos documentos se establece lo siguiente:
Fibras G.652 D: MFD o diámetro de campo modal a 1310nm comprendido entre 8,6 y 9,5 micrómetros con una tolerancia de +/- 0,6 micrómetros.
Fibras G.657 A2: MFD o diámetro de campo modal a 1310nm comprendido entre 8,6 y 9,2 micrómetros con una tolerancia de +/- o,4 micrómetros.
Por lo tanto, si que es cierto que en un caso extremo una fibra G.652 D podría llegar a tener un MFD de tan solo 8 micrómetros mientras que las fibras G.657 A2 no pueden tener un MFD inferior a 8,2 micrómetros, pero en cambio, una G.652 D también puede llegar a tener un MFD de 10,1 micrómetros, mientras que una G.657 A2 no pasará en ningún caso de 9,6 micrómetros.
A la vista de los datos anteriores, se puede discrepar sobre cual de los dos tipos de fibras tiene un menor MFD, pero eso no influye en la explicación dada sobre que es realmente el MFD de una fibra óptica monomodo y porqué los fabricantes cuando hablan de fibras monomodo dan este valor y no el diámetro del núcleo, tal y como sucede con las fibras multimodo.
Un saludo
Enrique del Rio
CIFP Tartanga LHII
Erandio
Bizkaia
Esto esta mal explicado la fibra 652D es menor diamtro al de 657 A2.
Enrique, gracias por tu respuesta y disculpas en la demora en este agradecimiento.
Me queda claro con tu explicación el motivo y ya no quedan dudas.
Saludos!
Hola Nahuel
Las pérdidas en una fibra óptica se deben a dos tipos de causas, las causas intrínsecas o relacionadas con el proceso de construcción de la fibra óptica y las causas extrínsecas o relacionadas con los procesos de instalación. Las causas intrínsecas se deben fundamentalmente a las impurezas que quedan en las fibras en el proceso de fabricación y son mayores cuanto menor es la longitud de onda respecto al tamaño de las impurezas. Estas pérdidas intrínsecas aparecen representadas en la gráfica donde se muestran las ventanas de trabajo de un fibra óptica y donde se ve claramente que, a menor longitud de onda, mayores son las pérdidas. En el propio blog de fibra óptica tienes una entrada donde aparecen explicadas este tipo de cosas.
Fundamentos de las fibras ópticas
Es decir, las pérdidas no tienen nada que ver con el diámetro de campo modal. Si el diámetro de campo modal de una fibra es mayor que el de otra, podrá aceptar más cantidad de luz por dicha fibra, pero luego las pérdidas que sufra esa luz dependerán de las impurezas de la fibra y de la longitud de onda utilizada.
El diámetro de campo modal si que puede influir en las pérdidas extrínsecas, que son debidas al propio proceso de instalación. Si no se tiene en cuenta este valor y se fusionan dos fibras monomodo de diferentes diámetros de campo modal, en uno de los sentidos de transmisión de la luz las pérdidas en esa fusión serán superiores a las previstas, tal y como se muestra en una de las imágenes de la entrada del blog que habla de este tema.
Espero haber aclarado tu duda.
Un saludo
Enrique del Rio
CIFP Tartanga
Erandio
Bizkaia
Hola. Lo que no logro entender es por qué en la G652D, si el diámetro de campo modal a 1310nm es menor que a 1550nm, la atenuación es mayor a 1310nm. Por ejemplo, en algunas fibras, e incuso en la que se usa de ejemplo en este artículo, el diámetro de campo modal a 1310 es de 9.2 y a 1550nm es 10,3, si el núcleo es de 8,2, por qué hay mayor atenuación a 1310nm? no debería ser alreves considerando que a 1550nm hay una mayor porción de la onda que viaja por fuera del núcleo?
Muy bueno, gracias!
Excelente aporte, muchas gracias por el tema, es muy pertinente.
Muchas gracias por sus explicaciones, estoy capacitandome en redes ópticas y esto me ha servido mucho
Muy interesante y aclaratorio…gracias
Esta entrada me ha parecido muy interesante!!!